定义
关系闭包是
- 一个 关系 $\to$ 关系 的函数
- 保留原关系
- 对所有原来元素/关系拥有某种关系
数学定义:关系 $U$ 的闭包 $u(R)$ $:=$
- $u(R)$ 满足 $U$
- $R \subset u(R)$
- $\forall R\subset S$ 且 $S$ 满足 $U$ $\implies$ $u(R) \subset S$
常见闭包

- 自反闭包 $r(R) = R \cup \Delta_{A}$
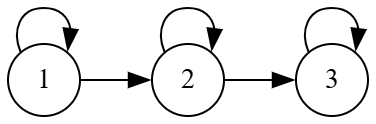
- 对称闭包 $s(R) = R \cup R^{-1}$
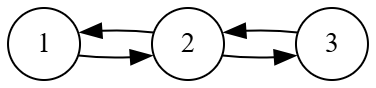
- 传递闭包 $t(R) = \bigcup_{k=1}^{\infty}R^{k}$
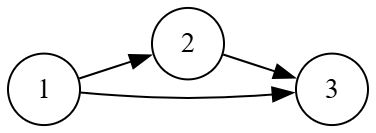
性质
换序
- 交
- $r(R \cap S)=r(R) \cap r(S)$
- $s(R \cap S) \subset s(R) \cap s(S)$
- $t(R \cap S) \subset t(R) \cap t(S)$ 利用 $t(R\cap S)=t(\emptyset)=\emptyset$ 构造反例
- 并
- $r(R \cup S)= r(R) \cup r(S)$
- $s(R \cup S)= s(R) \cup s(S)$
- $t(R \cup S) \supset t(R) \cup t(S)$
性质保持
| 闭包 | 自反闭包 $r$ | 对称闭包 $s$ | 传递闭包 $t$ |
|---|---|---|---|
| 保持自反性 | ✅ | ✅ | ✅ |
| 保持对称性 | ✅ | ✅ | ✅ |
| 保持传递性 | ✅ | 反例 {(1,2)} | ✅ |