码制
🔗码制
!码制
定点数
定点整数
- 首位为符号位
- 小数点在末尾
定点小数
- 表示纯小数
- 首位为符号位
- 小数点在开头
浮点数
IEEE754
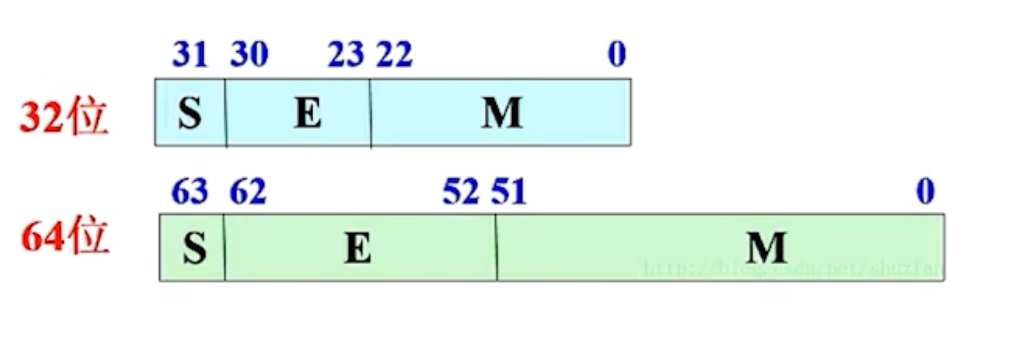
- $S:=$ 符号位
- $E:=$ 阶码 (移码)
- $M:=$ 尾数 (原码)
float $=(-1)^{S}\times 2^{E-127} \times(1.M)$ = [1:8:23]
double $=(-1)^{S}\times 2^{E-1023}\times(1.M)$ = [1:11:52]
移码
已知原码 $e$ 位数为 $k$
则其移码 $E$ 满足 $$E=e+2^{k-1}-1$$
偏置值 $\mathrm{Bias}=2^{k-1}-1$
阶码原码范围 $-\mathrm{Bias}+1\leq e\leq \mathrm{Bias}$
特殊浮点数
| 特殊数类型 | 阶码 | 尾数 | 注意 |
|---|---|---|---|
| $\pm 0$ | 全 0 | 全 0 | 因此 $1.0\times2^{-127}$ 实际上是 $0$ 最小的正规格化数是 $1.0\times2^{-126}$ |
| $\pm \infty$ | 全 1 | 全 0 | |
| 非规格化数 | 全 0 | 非全 0 | |
| 非数 NaN | 全 1 | 非全 0 |
| 正负 | 绝对值 | 单精度值 | 双精度值 | 公式 |
|---|---|---|---|---|
| 正 | 最大 | $(2-2^{-23})\times2^{127}$ | $(2-2^{-52})\times2^{1023}$ | $(2-2^{-\lvert M \rvert})\times2^{\mathrm{Bias}}$ |
| 正 | 最小 | $1\times2^{-126}$ | $1\times2^{-1022}$ | $1\times2^{\mathrm{Bias}-1}$ |
| 负 | 最大 | $-(2-2^{-23})\times2^{127}$ | $-(2-2^{-52})\times2^{1023}$ | $-(2-2^{-\lvert M \rvert})\times2^{\mathrm{Bias}}$ |
| 负 | 最小 | $-1\times2^{-126}$ | $-1\times2^{-1022}$ | $-1\times2^{\mathrm{Bias}-1}$ |