也是一种广义 感知机

构成

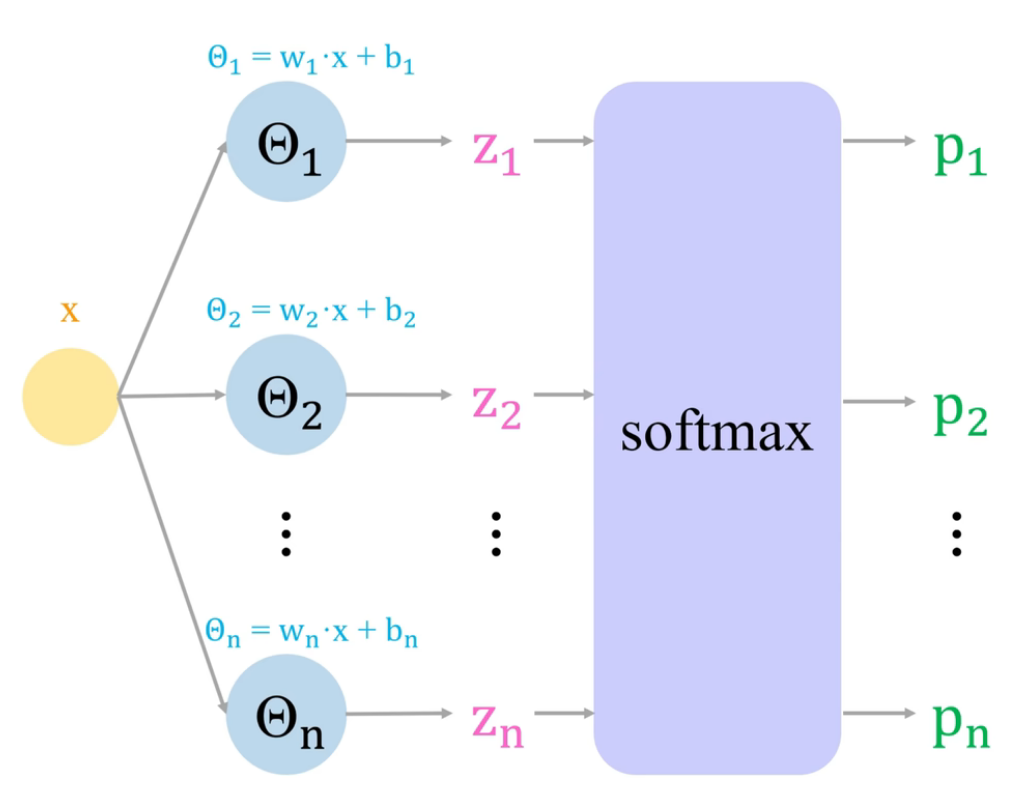
• 线性部分: $$\boldsymbol{y}=W\boldsymbol{x}+\boldsymbol{b}=\begin{bmatrix}w_{1} \ w_{2} \ \vdots \ w_{m}\end{bmatrix}\boldsymbol{x}+\boldsymbol{b}$$
• 激活函数: $$\mathrm{softmax(\boldsymbol{y})}$$

损失函数

用 交叉熵 作为损失函数

$$ \boldsymbol{L}=\frac{1}{T}\sum_{j=1}^{T} \mathrm{Entropy}(\boldsymbol{y}^{(j)},\hat{\boldsymbol{y}}^{(j)}) $$

即 $$ \boldsymbol{L}=-\frac{1}{T}\sum_{j=1}^{T} \boldsymbol{y}^{(j)}\cdot \log_{2}\hat{\boldsymbol{y}}^{(j)} $$ aka $$ L_{i}=-\frac{1}{T}\sum_{j=1}^{T} y_{i}^{(j)}\cdot \log_{2}\hat{y}{i}^{(j)} $$ 代入 softmax 后为 $$ L{i}-\frac{1}{T}\sum_{j=1}^{T} y_{i}^{(j)}\cdot \log_{2} \frac{\exp(w_{i}x^{(j)})}{\sum_{c=1}^{n} \exp(w_{c}x^{(j)})} $$